ミルキヅクのブログ

交点はなぜ解になる？

数学

ｘ軸上の交点

関数グラフとｘ軸との交点は解になる。

なぜだろう？

そこで、まず $f\left( x\right) =x^{2}$ を準備する。

$f\left( x\right)$ とは、ｘに、ある値を入れた時のｙの値。

だから $f\left( x\right)=y$

よって、 $f\left( x\right) =x^{2}$ は次のようになる。

$f\left( x\right) =y=x^{2}$

$f\left(x\right)=0$ とは、ｘに、ある値を入れた時のｙが常に0という意味。つまりｘ軸のこと。

$「f\left(x\right)=0」=\text x軸$

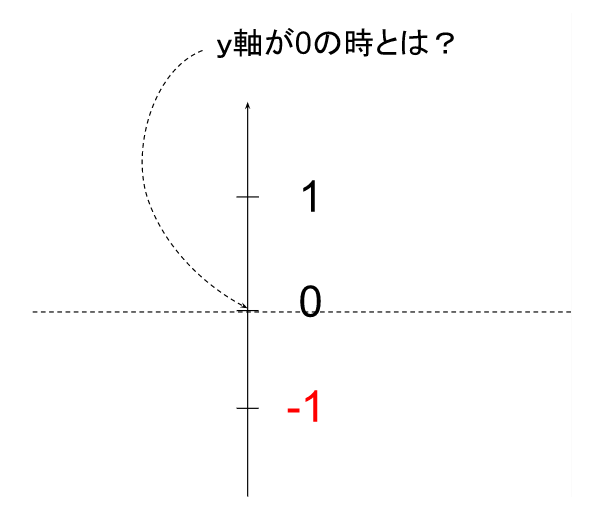
$f\left(x\right)=0$ とは、ｙ＝0のこと。

よって、以下の２つの関数は、

$f\left( x\right) =x^{2}$

$f\left(x\right)=0$

以下の２つの方程式となる。

$y=x^{2}$
$y=0$

この連立方程式を解くと、

$x^{2}=0$

よって、

$x=0$

それが、 $f\left( x\right) =x^{2}$ のグラフとｘ軸との交点である。

つまり、（ｘ,ｙ）=（0,0）

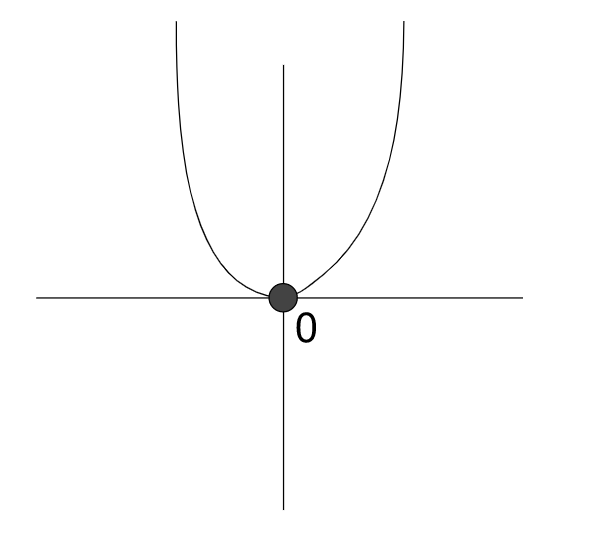
では、交点がはっきりわかる $f\left( x\right) =x^{2}-1$ でも見てみよう。

ｘ軸に交点が２つある。

この交点のｘ軸は、1と-1である。

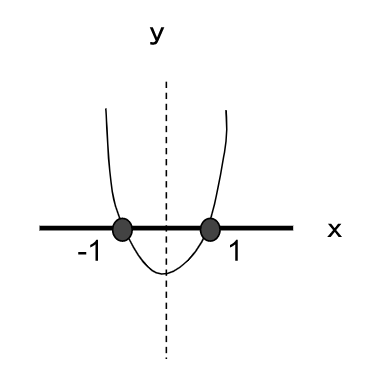
$y=x^{2}-1$ と $y=0$ であるｘ軸は交差している。

$y=x^{2}-1$ のｙに0を入れると、ｙが0の時のｘの値が求まる。

計算すると、

$0=x^{2}-1$

$x^{2}=1$

2乗して１になるのは、1と-1。

たしかに、ｘ軸との交点になっている。

$y=x^{2}-1$ のｙに0を入れるとは？

ｙ＝0とはｘ軸のこと。

$y=x^{2}-1$ は、一見１つの式に見えるが、

ｘ軸（y=0）も方程式と捉えることで、下記の連立方程式を作っていることを意味する。

$y=0$ 　（ｘ軸のこと）

$y=x^{2}-1$

ポイント

ｙ＝0とは、ｙ＝0（ｘ軸）との連立方程式を解くこと。

ｙ軸上の交点

では、ｙ軸との交点はどうだろう？

ｙ軸と $y=x^{2}-1$ の交点は、ｙ＝-1となるだろうか？

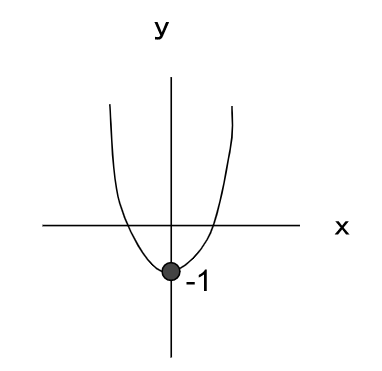
ｙ軸とは、 $f\left( y\right) =0$ という関数。

ｙにどんな値を入れてもｘが0。

つまりｘ＝0という方程式。

xy軸において、 $f\left( y\right)$ が求めている未知数は、ｘ。

そこで、ｘ＝0（ｙ軸）と、 $y=x^{2}-1$ との連立方程式を解くと

$x=0$ …①

$y=x^{2}-1$ …②

ｙ＝-1となった。

（ｘ,ｙ）＝（0,-1）という交点になっている。

交点の意味

交点があるとは、解があること。

虚数とは？

では交点がなければ、解（答え）がないということか？

$y=x^{2}$ の曲線を上に１つ動かした $y=x^{2}+1$ で考えてみよう。

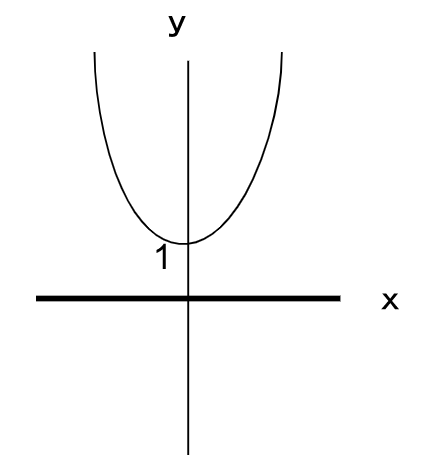
ここでｙ＝0の時ｘの値は何になるか？

ｘ軸との交点はないので、解はなさそうだ。

確かめてみよう。

$f(x)=\left( x^{2}+1\right)=0$

$\left( x^{2}+1\right)=0$

両辺に-1すると

$x^{2}=-1$

ある数を自乗してマイナス1になる数。

そのような実数はない。

従って実数において、解（答え）はない。

今まで説明しているｘｙ座標は実数の中での話。

数には、実数以外に、虚数という領域もある。

ルートの中がマイナスの値を虚数という。

自身をかけてマイナスになるという不思議な世界。

イメージしにくい世界であるが、虚数の世界まで解の範囲を世界を広げると虚数解がある。

虚数は虚構の数ではなく、実用的に使われているリアルな数だ。

補足： $\sqrt{-1}$ は虚数。 $i$ で表現する。

$i$ は $\sqrt{-1}$ 　よって、 $i^{2}=1$ 　

$i \times i =\sqrt{-1} \times \sqrt{-1}=1$

数の概念

ところで実数とは何か？

人は数の概念を広げてきた。

1.2.3と指で数えられる「自然数」

自然数に0とマイナスを含めた「整数」

次に「分数」や「小数」

分数の中でも、整数で分母分子が構成される「有理数」（分母が0の時だけは除く）

そうでない「無理数」

それら全体を「実数」と呼ぶ。

実数の世界にない数が「虚数」

実数と虚数を合わせて「複素数」

補足：上記の概念が曖昧だと、問題文を読んだ時に、その用語を見ただけで難しく感じる。特に、有理数と無理数の違い。

有理数と無理数の違い

無理数は、何が無理かといえば、比で表すことが無理と言っている。

有理数は英語でrational number。

rationalは合理的という意味があるが、語源のratioとは割合。

つまり、比がある数だと言っている。

一方、無理数はIrrational（＝not rational）

つまり比で表せない数と言っている。

有理数とは、0を除く整数で表せる数のこと。

無理数のように数が永遠に続くと、１に対する比が確定できない。

たとえば

$\dfrac{\sqrt{2}}{1}$

これは、

$\sqrt{2}:1$ で、１に対して $\sqrt{2}$ という比に見える。

しかし、 $\sqrt{2}$ は終わりなき数だから、１に対する比が永遠に定められない。

いやいや、 $\sqrt{2}$ で確定しているでしょ？

と思うかもしれないが、 $\sqrt{2}$ という数は無限に測れる計量器があったとしたら、永遠に数字が確定されない。

一方、0.111…や0.222…のような循環小数も、終わりなき数に見えるがちゃんと、 $\frac{1}{9}$ や $\frac{2}{9}$ という整数のコンビネーションで表せる。（だから、有理数というのだが…。 $\frac{1}{9}$ は1：9　 $\frac{2}{9}$ は2：9という比で表せる。）

整数１も確かに、1.000と0が続いてはいえるが、たとえば、整数の１は、１で完結している。計量器にのせても1.000…と表示され計量は終わる。

方程式同士の交点

$f\left( x\right) =x$ と $f\left( x\right) =1$

ｘ軸やｙ軸を方程式とみなして交点を求めることができた。

とうぜん、次の２つの関数でも交点が解になりそうだ。

$f\left( x\right) =x$

$f\left( x\right) =1$

つまり、方程式でいえば、

ｙ＝ｘ

ｙ＝1

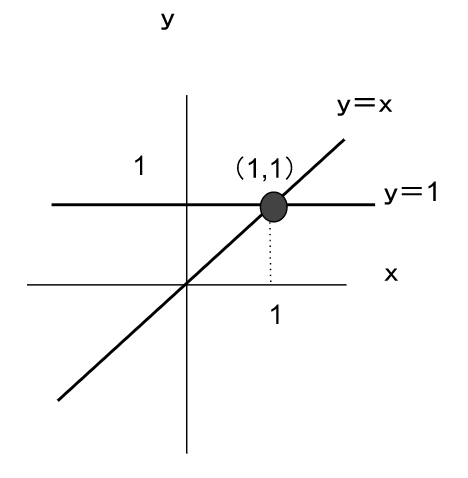
２つの連立方程式を解くと

ｘ＝1

ｙ＝1

２つの方程式の交点は（1,1）と求まった。

$f\left( x\right) =x$ と $f\left( y\right) =1$

$f\left( y\right) =1$ とは、yにどんな数字を入れてもxが１。

つまりx＝１の線。

同じく連立させるだけ。

$y=x$

$x=1$

よって

x=1　y=1

交点は（1,1）。

以上のようなｘｙ座標は哲学者でもあり数学者でもあったデカルトが考えた発明品。

これにより、交点を求めるだけでなく、形や物の動きが数で表せるようになった。

いわば、形で未知数を解く「幾何（きか）」と、数や記号で未知数を解く「代数」の融合である。

蛇足：幾何という訳はわかりにくい。

要は、

図形的なアプローチ⇒　幾何

記号と数を使ったアプローチ⇒　代数

アプローチとは、未知数を求めること。数学は、未知数を求める学問。

Copyright (C)　ミルキヅク All Rights Reserved.